Optical simulations of bifacial PV cells and modules

Malte Ruben Vogt, Carsten Schinke, Karsten Bothe; Institut für Solarenergieforschung GmbH (ISFH), Germany

Bifacial PV cells and modules convert light incident onto the front as well as the rear side. The ability to use light incoming from the rear side for the generation of electrical current enables bifacial modules to have higher energy yields than monofacial modules under equal conditions [1][2]. The "international road map for photovoltaics" [3] predicts an increase in market share for bifacial cells and modules from 2% in 2016 to above 30% within the next ten years. In order for this prediction to become reality, fast and accurate simulation tools for bifacial PV cells, modules and power plants are required.

Optical simulations of bifacial PV devices are more complex compared to simulations of monofacial devices since light incident onto the rear surface must be considered as well. Moreover, the optical properties of objects behind the devices have to be included since light may be transmitted through and reflected back into the device from the rear. The necessity of taking the reflectance of objects behind the solar cell into account is evident from experimental observations [2][4].

An effective numeric simulation model needs to balance the required accuracy of the results against the computational requirements. This is commonly achieved by focusing on a sufficiently accurate description of relevant physical effects while neglecting those effects of minor impact on the results. Applying this principle to bifacial PV devices leads to splitting the simulation into two different types, depending on the focus of the optical simulation. If the goal of the simulation is to understand or improve the optical properties of bifacial solar cells and modules, then optical properties of the cells and other module components are modeled in steady state conditions and with wavelength resolution. Often, standard testing conditions as present in indoor testing laboratories are assumed for this purpose. However, if the goal of the simulation is to calculate the energy yield of a module or an entire power plant at a given location over a certain time, then the modules themselves are modeled in less detail and the focus is shifted to the mounting environment and the incoming irradiation. In this case, wavelength effects are usually neglected, but time dependence needs to be taken into account. The issues considered in the following are discussed in more detail in Ref. 5.

1. Optical simulations of bifacial PV cells and modules indoors

Modeling the optics of solar cells and modules must address the following physical effects, which are visualized in Figure 1:

• Refraction of light at interfaces between different materials (rays 2-9),

• Reflection of light at interfaces between different materials (rays 1, 3, 6, 7),

• Absorption of light within materials (rays 2, 4, 5, 8, 9),

• Scattering of light at rough surfaces (ray 6),

• Interference at thin films, e.g., anti-reflection coatings (ray10),

• Diffraction, e.g, at surface textures (ray 11).

Figure 1: Optical effects in a PV module: Refraction (2-9), diffraction (11), reflection (1, 3, 6, 7), absorption (2, 4, 5, 8, 9), scattering (6) and interference (10).

Ray tracing [5][6][7][8] simulations are often used when simulating complex PV devices as shown in Fig. 1. The basic idea of optical ray tracing simulations is the calculation of the propagation of single light rays with various directions through a scene. The light rays are emitted by a light source and ray parameters such as intensity and direction are continuously monitored. When the light ray interacts with an object within the scene, a refraction calculation is performed (e.g., based on refractive index data and the morphology of the object's surface) and the ray parameters are adjusted accordingly. This process is continued until the ray is absorbed or leaves the scene. In this case, the ray tracer records the termination parameters, e.g., position of absorption, and the process is restarted with another ray. Often, rays are emitted with random direction and wavelength. Repeating the simulation for a large number of rays then yields an estimation for the average interaction of light with the objects in the simulation.

Ray tracing models for photovoltaics have to deal with the interaction of light with objects whose size scale is on six different orders of magnitude. For instance, a PV module has to be modeled on the order of meters. In contrast, the lateral extent of solar cells in the module is of the order of centimeters, whereas their thickness is of the order of 100-200 microns. Surface textures, which alter the optical properties of solar cells significantly, are of the order a few microns. Combining these different size scales in one ray tracing simulation while restricting the computational effort to a reasonable amount is a challenging task.

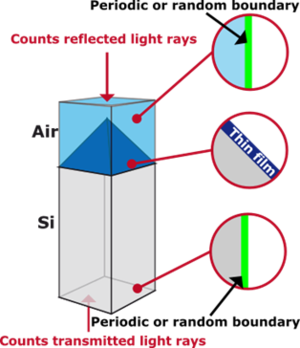
For solar cells, a common ray tracing approach is the consideration of a simulation domain consisting of one element of the texture (e.g., a pyramid) and the part of the solar cell below, as depicted in Figure 2. The simulation domain then has dimensions of the order of 5 µm × 5 µm × 170 µm. Periodic boundary conditions are applied, which means that infinite lateral extent of the solar cell is assumed. This assumption is usually justified: Typical solar cells have a lateral extent of 156 mm, which is more than four orders of magnitude larger then the lateral extent of the simulation domain. Due to the periodic boundary conditions, this simulation describes solar cells with a regular structure of surface texture. However, solar cells with random textures can also be described by introducing a random displacement of the ray after application of the periodic boundary condition. This approach is sometimes called random boundary condition and is used by many solar cell ray tracing programs such as Sunrays [6], the PV lighthouse wafer ray tracer [7] or the Sentaurus raytracer [8].

Figure 2: Classical simulation domain for Si based solar cells.

The simulation of bifacial PV devices s requires an adaptation of the rear side of the simulation domain, i.e.: Addition of rear side texture, materials below the cell and eventually a light source at the rear side of the cell. This can lead to two separate simulations (one with the light source positioned in front of and another one with the light source positioned behind the PV device) or the simultaneous use of two light sources in one simulation. In the first case, the simulation results need to be combined in an appropriate post processing step. The second option requires a simulation tool which is capable of using multiple light sources with correct relative intensities. For an optical loss analysis, it may be helpful to distinguish between light rays originating from either of the two light sources.

A limitation of the common simulation domain described above becomes obvious when trying to integrate the metalized contacts into the simulation domain, since the metallization structures are much larger than the domain. The front surface metallization is therefore usually not considered in the ray tracing simulation itself but taken into account during post processing of the simulation results by reducing the determined short circuit current of the solar cell by the fraction of metalized (shaded) front surface area. The symmetry of simulation domains as in Fig. 2 is also broken for bifacial PV devices, since they have localized metal structures on the rear side. These rear side metal contacts change the optical properties of the rear side locally, but on a size scale larger than the texture, which determines the domains width.

Figure 3: Multi-domain-approach for bifacial modules. From the perspective of the light rays (red lines), the way through the different domains needs to represents the path through a real PV module.

In order to simulate the interaction of light with a PV module appropriately, not only light hitting the solar cells must be considered, but also light hitting the gaps between the solar cells. This can be achieved by using a multi-domain approach [9] as illustrated in Figure 3. In the multi-domain approach, the simulation scene is split into several domains. Each domain contains one symmetry element (modeled in three dimensions) and appropriate boundary conditions to represent its periodic or random lateral repetition. In order to enable interaction between objects in different domains, there needs to be a way for the light rays to travel from one domain to another. From the perspective of the light ray, the way through the different domains needs to represents the path through a real PV module. Depending on the cell architecture, up to five domains are required for a representation of a PV module. The first (top-level) domain is called "module domain". It is irradiated by the light source and contains one whole solar cell and its surrounding components in the module. The second domain is the "front finger domain". It contains the symmetry element surrounding one front finger. The third domain is the "front texture domain". It contains the symmetry element of the surface texture and its surroundings. Depending on the cell architecture, a "rear texture domain" and a "rear finger domain" are also used. Each of these domains apply periodic or random boundary conditions at their side faces (green lines). In contrast, top and bottom faces of domains b)-e) are connecting the domains. One option for a practical realization of this connection are surface effects (magenta lines) which shift light rays from one domain to another.

Figure 4 shows the ray tracing results for a typical bifacial module illuminated by a front light source. The orange area represents the fraction of the light converted into electrical current. The two biggest losses are the reflection of all the module's components (green) and transmission through the module (magenta). The other losses are absorption by parts of the module other than the cell's absorber (e.g. glass or metallization), which are converted into heat.

Figure 4: The results of the interaction of the incoming light with a typical bifacial module. The orange area represents the fraction of the light converted into electrical power. Cumulated, the two biggest losses are the reflection of all the module's components (green) and transmission through the module (magenta).

2. Optical simulations of bifacial PV modules and power plants outdoors

Outdoors, the irradiation depends on the location, time and weather. Thus, the light source must either generate radiation representing irradiation conditions which are averaged over the whole year [10] or specific irradiation for each hour of the year [2][11]. The second option requires a post-processing step in order to combine the simulation results over the whole year.

Modelling the interaction of the module with its environment correctly requires the mounting height and angle to be included in the simulation domain (see Fig. 5a). Additionally, other objects that might block or reflect light, such as ground, trees, buildings or the mounting rack, need to be included in the simulation model as well.

Figure 5: Simulation domain for modelling the interaction of the module with its environment. a) The mounting height and angle of a module. b) The light rays can hit the module front and rear side directly or after reflection from the ambience.

Since the energy yield of bifacial and monofacial PV devices can be very similar under front side illumination [12], the possible advantage of bifacial modules is often quantified be the bifacial gain G_bif , which is the current generated by light incoming from the rear side I_rear divided by the current generated by light incoming from the front side of the PV device I_front :

[math]\displaystyle{ G_{bif} = \frac {I_{rear}} {I_{front}} }[/math] (1)

The average annual current of a PV device is the current generated under illumination by a light source representing irradiation conditions which are averaged over the whole year [10][13]. The average annual current facilitates a current rating for PV modules. A current rating can be used to evaluate the optical performance of PV modules under certain reference irradiance and mounting conditions. Analogously to Eq. (1), a "bifacial average annual current gain " [13] can be defined as Ḡ_bif:

[math]\displaystyle{ \bar{G}_{bif} = \frac {\bar{I}_{rear}} {\bar{I}_{front}} }[/math] (2)

Figure 6: Average annual current gain of bifacial modules compared to monofacial modules.

Figure 6 shows the average annual bifacial current gain for different mounting heights and ground materials according to [13]. The simulations are conducted for a module facing south at a 35° tilt angle (see Fig. 5a) with the average yearly irradiation conditions in Hamelin, Germany. The results for a ground reflection of zero (Fig. 6, magenta) show, that a bifacial gain of 3.6%abs is achieved due to light which hits the rear side of the module without being reflected at the ground before (see light paths Fig. 5b). Consequently, this 3.6%abs gain is independent from the module mounting height. The bifacial gains due to reflection from the ground are dependent on the ground albedo and on the module mounting height. For the bifacial module simulated above the white underground, a 10%abs increase in average annual current is achieved by mounting it 1 m above the ground instead of 0.1 m. Making the same change in mounting height above green grass or asphalt only leads to a 4%abs or 1%abs increase in average annual current, respectively. This demonstrates that high ground reflectivity increases the current gain caused by higher mounting heights. This is a consequence of the larger ground area "seen" by the module when increasing its mounting height.

References

[1] A. Cuevas, A. Luque, J. Eguren, and J. del Alamo, "50 Per cent more output power from an albedo-collecting flat panel using bifacial solar cells," Sol. Energy, vol. 29, no. 5, pp. 419-420, 1982.

[2] G. J. M. Janssen, B. B. Van Aken, A. J. Carr, and A. A. Mewe, "Outdoor Performance of Bifacial Modules by Measurements and Modelling," Energy Procedia, vol. 77, pp. 364-373, 2015.

[3] "International Technology Roadmap for Photovoltaic (ITRPV)," no. Eighth Edition. 2017.

[4] C. Deline, S. Macalpine, B. Marion, F. Toor, A. Asgharzadeh, and J. S. Stein, "Assessment of Bifacial Photovoltaic Module Power Rating Methodologies-Inside and Out," IEEE J. Photovoltaics, vol. 7, no. 2, pp. 575-580, 2017.

[5] C. Schinke, M. R. Vogt, and K. Bothe, "Optical Modeling of Photovoltaic Modules with Ray Tracing Simulations," in Photovoltaic Modeling Handbook, 2018, pp. 27-92.

[6] R. Brendel, "Sunrays: A versatile tracing program for the photovoltaic community," in 12th EUPVSEC, 1994, no. April, pp. 1339-1342.

[7] P. Lighthouse, "Wafer ray tracer." [Online]. Available: https://www2.pvlighthouse.com.au/calculators/waferraytracer/waferraytracer.html.

[8] Synopsys Incorparation, "Sentaurus Device." Mountain View, CA, USA.

[9] M. R. Vogt et al., "PV module current gains due to structured backsheets," Energy Procedia, vol. 124, pp. 495-503, Sep. 2017.

[10] M. Winter, H. Holst, M. R. Vogt, and P. P. Altermatt, "Impact of realistic illumination on optical losses in Si solar cell modules compared to standard testing conditions," in 31st EU PVSEC, 2015, pp. 1869-1874.

[11] U. A. Yusufoglu et al., "Simulation of energy production by bifacial modules with revision of ground reflection," Energy Procedia, vol. 55, pp. 389-395, 2014.

[12] T. Dullweber et al., "Present status and future perspectives of bifacial PERC + solar cells and modules," Jpn. J. Appl. Phys., vol. 57, no. 08RA01, 2018.

[13] M. R. Vogt, T. Gewohn, K. Bothe, C. Schinke, and R. Brendel, "IMPACT OF USING SPECTRALLY RESOLVED GROUND ALBEDO DATA FOR PERFORMANCE SIMULATIONS OF BIFACIAL MODULES," in Proc. 35th European Photovoltaic Solar Energy Conference and Exhibition, 2018, pp. 1011-1016.