Differential spectral responsivity (DSR) method
Ingo Kroeger
Introduction
The DSR-method is a spectral method using quasi monochromatic light as a light source. Hence, for this method a reference is needed with calibrated differential spectral irradiance responsivity. This could be a reference solar cell or a photodiode. The optical setup of a DSR-facility is typically built up the following way: A white light source such as a Xe arc lamp or a halogen lamp is coupled into a monochromator system that selects the desired wavelength. Following the monochromator there is an optical chopper that modulated the monochromatic light with a given frequency f. Subsequently the monochromatic light passes an imaging optics that generates a uniform irradiance distribution in the measurement plane. Within this optics there is a beam splitter that couples a fraction of the monochromatic light onto a monitor photodiode. Finally, there are white light bias lamps that can generate a bias irradiance between 0 – 1100 W/m² in the measurement plane additionally to the monochromatic irradiance. The DUT and the reference must be temperature controlled and kept at 25°C. Both reference device and DUT shall be connected to a transimpedance amplifier, that coverts the currents into voltages and keeps the solar cell in short circuit state. The AC modulated voltage generated by the monochromatic spectral irradiance shall be then measured by a Lock-In amplifier, the DC voltage generated by the bias irradiance shall be measured by a calibrated multimeter. Also the Monitor current should be converted into a voltage using a shunt or a transimpedance amplifier and measured by a Lock-In-amplifier. The calibration procedure would be as follows:
The DSR-calibration procedure
A constant irradiance responsivity s=Isc(E)/E is determined from short-circuit current Isc(E) and associated irradiance E. However, for a reference solar cell with non-linear behavior, the differential irradiance responsivity [math]\displaystyle{ \widetilde{s}(E_{b}) }[/math] in the presence of a bias irradiance Eb must be taken into account.
[math]\displaystyle{ \widetilde{s}(E_{b})= \frac {\delta I_{sc}(E)} {\delta E} | E_{b} }[/math]
Spectrally resolved (wavelength ), the differential spectral irradiance responsivity [math]\displaystyle{ \widetilde{s}(\lambda , E_{b}) }[/math] provides the basis for the calculation of the quantities to be calibrated, taking prescribed standard test conditions (index STC) into account. It is determined by spectroradiometry in accordance with the DSR method (differential spectral responsivity method).
The DSR method is a two-beam procedure and makes simultaneous use of:
- a stationary bias irradiation with irradiances Eb which are not, however, explicitly measured. Its variation over more than 2 orders of maginitude causes short-circuit direct currents Isc(Eb) which are measured, as well as
- a quasi-monochromatic measurement radiation modulated with time. Its irradiance is determined with reference radiometers (silicon photodiode or radiation thermopile as a detector, depending on the spectral range) whose functional values of the spectral radiant power responsivities as well as their aperture size are traceable to national standards.
Measurants
a) The values of the two-dimensional function of the absolute differential spectral irradiance responsivity [math]\displaystyle{ \widetilde{s}(\lambda,I_{sc}(E_{b})) }[/math] are determined by
- variation of both the bias irradiance and the wavelength of the measurement radiation which is separated with the aid of a grating double monochromator. The radiation source is a tunable laser system.
- As measuring radiation at the wavelength λ, a quasi-monochromatic homogeneous radiation field is used, where the reference radiometer (without bias irradiation) and the reference solar cell (together with bias irradiation) are irradiated alternately.
b) The function of the differential irradiance responsivity [math]\displaystyle{ \widetilde{s}_{AMx}(I_{SC}(E_{b})) }[/math] assessed in accordance with AMx as a function of the short-circuit current is obtained after assessment of the differential spectral irradiance responsivity with a spectral irradiance Eλ,AMx (λ) and the integration over the whole wavelength range.
[math]\displaystyle{ \widetilde{s}_{AMx(I_{SC(E_{b})})}= \frac { \int_{0}^{\infty} \widetilde{s}(\lambda,I_{SC}(E_{b})) \cdot E_{\lambda , AMx}(\lambda)d\lambda } { \int_{0}^{\infty} E_{\lambda , AMx}(\lambda)d\lambda } }[/math]
c) The associated value of the short-circuit current under standard test conditions ISTC = ISC(ESTC) is obtained in accordance with the following formula by approximation of the upper integration limit ISTC so that the value of the integral furnishes the irradiance .
[math]\displaystyle{ E_{STC} = \int_{0}^{I_{STC}} \frac {dI_{sc}} {\widetilde{s}_{AMx(I_{SC})}} \text{with AMx = AM1.5} }[/math]
An integration of the reciprocal of the function of the differential irradiance responsivity [math]\displaystyle{ 1/\widetilde{s}_{AMx}(I_{SC}) }[/math] assessed in accordance with AMx, via the short-circuit current ISC up to the measured value of the short-circuit current ISC(Eb) as a solid upper integration limit furnishes the value assessed in accordance with AMx of the associated bias irradiance
[math]\displaystyle{ E_{b,AMx} = \int_{0}^{I_{SC}(E_{b})} \frac {dI_{sc}} {\widetilde{s}_{AMx(I_{SC})}} }[/math]
d) Accordingly, the function of the absolute spectral irradiance responsivity is determined under standard test conditions sSTC(λ) for each wavelength by integrating the function of the differential spectral irradiance responsivity [math]\displaystyle{ \widetilde{s}(\lambda,E_{b,AMx}) }[/math] up to the irradiance of the standard test conditions ESTC:
[math]\displaystyle{ s_{STC}(\lambda) = \frac {1} {E_{STC}} \int_{0}^{E_{STC}} \widetilde{s} (\lambda,E_{b,AMx}) dE_{b,AMx} }[/math]
Measurement conditions
- Standard test conditions according to IEC TS 61836:2016 and IEC 60904-3:2019: - The spectral irradiance Eλ,AMx (λ) for the assessment is given by the AM1.5 reference solar spectrum Eλ,AM1.5 (λ) - The total irradiance amounts to [math]\displaystyle{ E_{STC} = 1000 W \cdot m^{-2} }[/math] - The temperature of the reference solar cell amounts to 25 °C
- The temperature of the solar cell is measured with the incorporated Pt100 measuring resistor and constantly controlled to values in the interval (25 ± 0.2) °C, whereby the nominal value of the Pt100 resistor of 100 ohm at 0 °C is used as a basis. According to DIN IEC 60751:2008 a Pt100 measuring resistor has a resistance of 109,735 Ohm at 25°C. During the assessment, the photocurrents are corrected with the aid of the measured temperature coefficient to the value expected at 25 °C. The ambient temperature lies between 24 °C and 26 °C.
- During the measurement, the bias radiation is constant with time, illuminates the reference solar cell homogeneously and has a spectral distribution similar to that of the reference spectrum according to IEC60904-3.
- The measurement radiation illuminates the reference solar cell and is modulated by a chopper with 78.9 Hz. It is formed as a slightly divergent beam with an aperture angle between the marginal rays of maximally 5° and has a quasi-monochromatic spectral distribution which is adjusted in the spectral range 280 nm ≤ λ ≤ 1200 nm in steps of 5 nm, with a spectral bandwidth (full width at half maximum) of [math]\displaystyle{ \Delta \lambda = \{ \frac {\text{5 nm for 280 nm } \leq \text{ } \lambda \text{ } \leq \text{ 680 nm}} {\text{10 nm for 680 nm } \leq \text{ } \lambda \text{ } \leq \text{ 1200 nm}} }[/math]
- Measurement geometry: The effective front face of the actual solar cell is the reference plane for the irradiance, and the beam-alignment axis of the measuring radiation is aligned vertically and centrically to it.
- The short-circuit current is measured with a current-voltage converter which is connected with the four connections on the solar cell housing via two current and potential connections each (four-wire method) and keeps the terminal voltage smaller than 100 μV
Model equation
As outlined in the previous section, the basic measurant is two-dimensional function of the absolute differential spectral irradiance responsivity, since all other quatities such as the value of the short-circuit current under standard test conditions and the function of the absolute spectral irradiance responsivity is determined under standard test conditions is derived from it mathematically only.
In the following section the model equation for the determination of the absolute differential spectral irradiance responsivity is described.
Since the device under test (DUT) and the reference (Ref) are measured subsequently the monitor principle shall be applied in order to correct for the drift of the quasi-monochromatic irradiance between both measurements. For that purpose a fraction of the quasi-monochromatic irradiance is coupled onto a monitor detector (i.e. a photodiode). The current measurement of the monitor detector must be measured synchronized in time (i.e. by a triggered measurement) with the corresponding DUT or Ref measurement.
[math]\displaystyle{ \widetilde{s}^{DUT}(\lambda , I_{b})= \widetilde{s}^{Ref}(\lambda , I_{b,Ref}) \cdot \frac {\frac { \Delta I^{DUT} (\lambda , I_{b}) } { \Delta I^{DUT} _{Mon} (\lambda) } } {\frac { \Delta I^{Ref} (\lambda , I_{b,Ref}) } { \Delta I^{Ref} _{Mon} (\lambda) } } = \widetilde{s}^{Ref}(\lambda , I_{b,Ref}) \cdot \frac {Q^{DUT}(\lambda , I_{b}) } {Q^{Ref}(\lambda , I_{b,Ref}) } }[/math]
Corrections
The monitor corrected signal QDUT(λ,Ib) and QRef(λ,lb,Ref) needs additional correction parameters in order to compensate for systematic measurement deviations listed below:
[math]\displaystyle{ \widetilde{s}^{Ref}(\lambda , I_{b,Ref})= \widetilde{s}^{Ref}(\lambda) \cdot \frac {Q^{DUT}_{8}(\lambda , I_{bias}) } {Q^{DUT}_{8}(\lambda , I_{bias,Ref}) } }[/math]
[math]\displaystyle{ Q_{8} (\lambda) = Q(\lambda) \cdot c_{R}(\lambda) \cdot c_{non-u}(\lambda) \cdot c_{dist} \cdot c_{shadow} \cdot c_{T}(\lambda) \cdot c_{WL}(\lambda) \cdot c_{BW}(\lambda) }[/math]
cR(λ): correction function related to the amplifications factors of the current voltage converters connected to DUT, Ref and the monitor detector.
cnon-u(λ): correction function related to the non-uniformity of the monochromatoc light field.
cdist: correction factor related to the alignment of the reference planes of DUT and Ref
cshadow: correction factor related to shadowing of the active area of DUT and Ref, i.e. by contacting bars.
cT(λ): correction function related to the deviation from set temperature, i.e. 25°C.
cWL(λ): correction factor related to wavelength calibration of the monochromatic light source
cBW(λ): correction function related to bandwith effects of the monochromatic light source
These correction factors need to be determined and applied in order to determine the correct calibration value for [math]\displaystyle{ \widetilde{s}^{DUT}(\lambda , I_{b}) }[/math].
Uncertainties
Determining the measurement uncertainty is an integral part of a calibration. The measurement uncertainty analysis presented in the following is based on the methodology specified in the guide to the expression of uncertainty in measurement (GUM). We conduct an uncertainty analysis based on a Monte-Carlo approach as described in the GUM supplement 1. The basic idea of this approach is the recalculation of the measurement result [math]\displaystyle{ \widetilde{s}^{DUT} (\lambda , I_{b}) }[/math] many times, while all input quantities are altered on each iteration i according to their uncertainties, the uncertainty distribution functions and the underlying model of impact on [math]\displaystyle{ \widetilde{s}^{DUT} (\lambda , I_{b}) }[/math]. The resulting distribution of [math]\displaystyle{ \widetilde{s}^{DUT}_{MC,i} (\lambda , I_{b}) }[/math] then directly yields an estimate of its uncertainty.
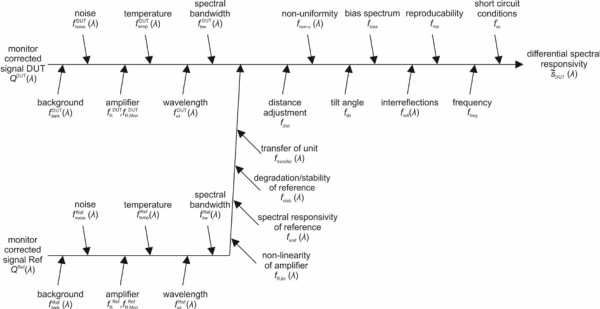
Figure 1 shows an Ishikawa diagram of all identified sources of uncertainty for the determination of [math]\displaystyle{ \widetilde{s}^{DUT} (\lambda , I_{b}) }[/math]. Each of these components affects the result of the measurement in a specific way, which can mathematically be expressed by a multiplicative f -factor:
[math]\displaystyle{ \widetilde{s}^{DUT}_{MC,i} (\lambda , I_{b}) = \widetilde{s}^{Ref}(\lambda) \cdot \frac {Q^{DUT}_{8} (\lambda , I_{bias})} {Q^{DUT}_{8} (\lambda , I_{bias,ref})} \cdot f_{MC,i}(\lambda) }[/math]
With:
[math]\displaystyle{ f_{MC,i}(\lambda) = \frac { f^{DUT}_{dark}(\lambda) \cdot f^{DUT}_{noise}(\lambda) \cdot f^{Ref}_{R}(\lambda) \cdot f^{DUT}_{R,Mon}(\lambda) \cdot f^{DUT}_{temp}(\lambda) \cdot f^{DUT}_{wl}(\lambda) \cdot f^{DUT}_{bw}(\lambda) \cdot } { f^{Ref}_{dark}(\lambda) \cdot f^{Ref}_{noise}(\lambda) \cdot f^{DUT}_{R}(\lambda) \cdot f^{Ref}_{R,Mon}(\lambda) \cdot f^{Ref}_{temp}(\lambda) \cdot f^{Ref}_{wl}(\lambda) \cdot f^{Ref}_{bw}(\lambda) \cdot } }[/math]
[math]\displaystyle{ f_{R,lin} \cdot f_{sref} (\lambda) \cdot f_{stab} (\lambda) \cdot f_{transfer} (\lambda) \cdot f_{dist} \cdot f_{non-u} (\lambda) \cdot f_{tilt} \cdot f_{bias} \cdot f_{refl} (\lambda) \cdot f_{rep} \cdot f_{freq} \cdot f_{sc} \cdot }[/math]
Figure 1: Ishikawa diagram of all sources of uncertainty for a DSR measurement.
These f-factors are as follows and shall desribe the following sources for uncertainty:
[math]\displaystyle{ f^{DUT}_{dark}(\lambda), f^{Ref}_{dark}(\lambda) }[/math]: Background subtraction.
[math]\displaystyle{ f^{DUT}_{noise}(\lambda), f^{Ref}_{noise}(\lambda) }[/math]: Measurement noise
[math]\displaystyle{ f^{Ref}_{R}(\lambda), f^{DUT}_{R}(\lambda), f^{DUT}_{R,Mon}(\lambda), f^{Ref}_{R,Mon}(\lambda) }[/math]: temperature coefficients of R, calibration of R, unknown R,…
[math]\displaystyle{ f^{DUT}_{temp}(\lambda), f^{Ref}_{temp}(\lambda) }[/math]: Accuracy of temperature sensor, Calibration of temperature sensor, temperature offsets, temperature non-uniformity
[math]\displaystyle{ f^{DUT}_{wl}(\lambda), f^{Ref}_{wl}(\lambda) }[/math]: reproducability of center wavelength, calibration of wavelength scale, offset of monochromator
[math]\displaystyle{ f^{DUT}_{bw}(\lambda), f^{Ref}_{bw}(\lambda) }[/math]: Uncertainty of Bandwidth correction model function, determination of true bandwidth
[math]\displaystyle{ f_{R,lin} }[/math]: non-linearity of transimpedance amplifier and Lock-In amplifier
[math]\displaystyle{ f_{sref}(\lambda) }[/math]: uncertainty of the reference detector
[math]\displaystyle{ f_{stab}(\lambda) }[/math]: drift/ageing of the reference detector
[math]\displaystyle{ f_{transfer}(\lambda) }[/math]: uncertainties if the reference detector is used in a different state than during its calibration
[math]\displaystyle{ f_{dist} }[/math]: Accuracy of relative alignment of Ref and DUT, Uncertainty of absolute position of reference plane in case of encapsulated devices
[math]\displaystyle{ f_{non-u}(\lambda) }[/math]: Uncertainty related to non-uniformity correction
[math]\displaystyle{ f_{tilt} }[/math]: uncertainty resuling from an relative angular misalignment between Ref and DUT
[math]\displaystyle{ f_{bias} }[/math]: uncertainty related to bias spectral distribution differs from the STC spectral distribution
[math]\displaystyle{ f_{refl}(\lambda) }[/math]: interreflections
[math]\displaystyle{ f_{rep} }[/math]: Reproducability, imperfectness of monitor principle
[math]\displaystyle{ f_{freq} }[/math]: uncertainties related to the applied chopping frequency
[math]\displaystyle{ f_{sc} }[/math]: deviation from short circuit state
All these sources of uncertainties have to be evaluated and quantified.
Example Calibration of a WPVS-reference solar cell at the Laser-DSR facility at PTB
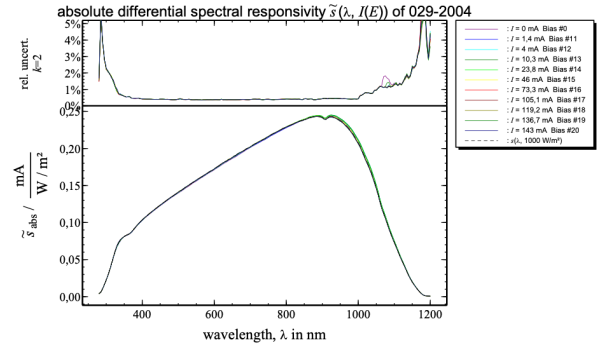
The Laser-DSR facility applies the abovemention DSR calibration procedure for WPVS reference solar cells. The model equation is applied to the measured data in order to determine the values of the two-dimensional function of the absolute differential spectral irradiance responsivity shown in Figure 2:
Figure 2: Calibration values of the absolute differential spectral irradiance responsivity of a WPVS reference solar cell.
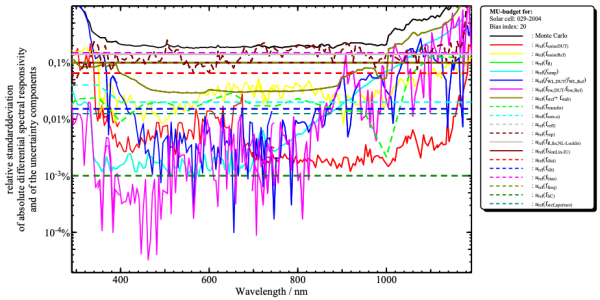
All of the abovementioned sources of uncertainties were carefully evaluated for this facility, quantified and applied in the uncertainty analysis based on a Monte-Carlo approach. An example compilation of these uncertainties is shown in Figure 3.
Figure 3 : Uncertainty contributions of a DSR measurement at LDSR-facility.
Propagating the uncertainties from the absolute differential spectral irradiance responsivity via the differential irradiance responsivity assessed in accordance with AMx to the value of the short-circuit current under standard test conditions resulted in an expanded uncertainty of 0,35% (k=2). Such a DSR measurement with lowest uncertainty can be ordered as calibration service for WPVS reference solar cells at PTB.
Summary
Within the scope of the 19ENG01 Metro-PV project “Metrology for emerging PV applications” a documented method for the traceable calibration of WPVS cells with an uncertainty of 0.35% using the laser-based differential spectral responsivity method was developed. The laser-based DSR setup at PTB for the primary calibration of reference solar cells was technically improved by improved fibre coupling, better amplifiers for the monitor device, improved cooling of bias lamps and usage of better reference spectroradiometers. An in-depth analysis of the transfer uncertainties from the primary reference photodiode to the solar cell (non-uniformity, stability, linearity) which lead to reduced transfer uncertainties.
A thourough model equation including a compilation of all sources of measurement uncertainties was developed and applied to the calibration procedure. Finally calibration of WPVS reference solar cells were performed resulting in expanded uncertainties of 0.35% (k=2) for the short circuit current at standard test condition. Such a DSR measurement with lowest uncertainty can be ordered as calibration service for WPVS reference solar cells at PTB.